
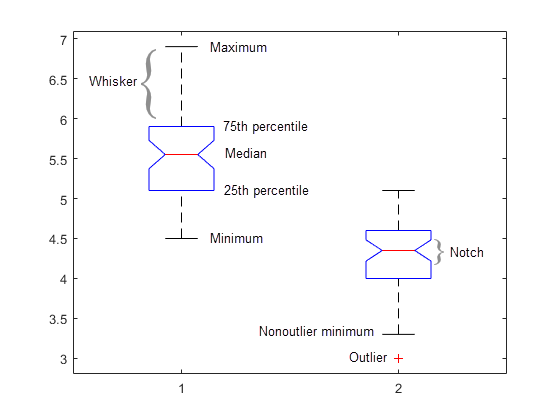
Otherwise, it is defined by \(Q_1 - 1.5 \times IQR\). So then, if the minimum of the sample is greater than \(Q_1 - 1.5 \times IQR\), then the lower whisker is defined by the minimum. This is provided that the size of the whisker is smaller than \(1.5 \times IQR\), where \(IQR\) is the interquartile range, and it is defined by \(IQR = Q_3 - Q_1\). Now, for the whiskers there is a rule to follow: the bottom whisker is defined by the minimum of the sample, and the top whisker is defined by the maximum of the sample. The top line of the box is defined by the third quartile (\(Q_3\)). The middle line of the box is defined by the median (\(Q_2\)). The bottom line of the box is defined by the first quartile (\(Q_1\)). In the graph above you have an example of a how a boxplot looks like: You have the "box" and the whiskers. When the minimum or maximum are too extreme, the "trim" the whisker and we annotate the existence of an outlier. Here, 1.5 IQR above the third quartile is 88.5 ☏ and the maximum is 81 ☏.The Box and Whisker Plot, or also known as Box-plot, is a type of graphical depiction of a sample, that provides easy to see key features of the distribution of a sample.Ī box-and-whisker plot provides the median as well as the first and third quartiles in its "box", and the minimum and maximum in the "whisker". The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Interquartile range (IQR) : the distance between the upper and lower quartiles.
In addition to the minimum and maximum values used to construct a box-plot, another important element that can also be employed to obtain a box-plot is the interquartile range (IQR), as denoted below: Third quartile ( Q 3 or 75th percentile): also known as the upper quartile q n(0.75), it is the median of the upper half of the dataset.First quartile ( Q 1 or 25th percentile): also known as the lower quartile q n(0.25), it is the median of the lower half of the dataset.Median ( Q 2 or 50th percentile): the middle value in the data set.Maximum ( Q 4 or 100th percentile): the highest data point in the data set excluding any outliers.Minimum ( Q 0 or 0th percentile): the lowest data point in the data set excluding any outliers.Same box-plot with whiskers drawn within the 1.5 IQR valueĪ boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles. Box plots can be drawn either horizontally or vertically.įigure 3. In addition, the box-plot allows one to visually estimate various L-estimators, notably the interquartile range, midhinge, range, mid-range, and trimean. The spacings in each subsection of the box-plot indicate the degree of dispersion (spread) and skewness of the data, which are usually described using the five-number summary. Outliers that differ significantly from the rest of the dataset may be plotted as individual points beyond the whiskers on the box-plot.īox plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying statistical distribution (though Tukey's boxplot assumes symmetry for the whiskers and normality for their length). In addition to the box on a box plot, there can be lines (which are called whiskers) extending from the box indicating variability outside the upper and lower quartiles, thus, the plot is also termed as the box-and-whisker plot and the box-and-whisker diagram.


In descriptive statistics, a box plot or boxplot is a method for graphically demonstrating the locality, spread and skewness groups of numerical data through their quartiles. Box plot of data from the Michelson experiment


 0 kommentar(er)
0 kommentar(er)
